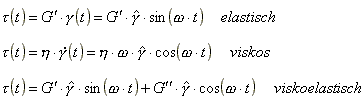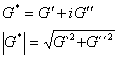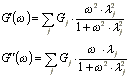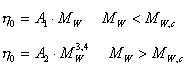Rheologiekurs - Teil 2


3. Instationäre Scherrheologie
3.1. Einführung
3.2. Relaxationsversuch
3.3. Kriechversuch
3.4. Oszillationsmessungen

3.1. Einführung

Wie im Abschnitt 1 angedeutet, zeigen Materialien neben viskosen auch mehr oder weniger starke elastische Eigenschaften. Das Verhalten der Materialien kann als Verschaltung einer Feder (elastische Eigenschaften) und einem Dämpfer (viskose Eigenschaften) aufgefasst werden. Man nehme eine Reihenschaltung von Feder und Dämpfer sowie eine plötzlich einsetzende Kraftwirkung an. Dann wird zunächst die Feder die Kraftwirkung aufnehmen. Erst nach und nach entspannt sich die Feder und die Dämpferbewegung setzt immer stärker ein. Bezogen auf die Dämpferbewegung erscheint diese Wirkung als eine Art Trägheit im Ansprechverhalten auf die Deformation. Der elastische Anteil kommt umso mehr zum Tragen, je kleiner die Deformationen sind und je schneller sie sich ändern. Bei langsamen Deformationen wird die Feder nur geringfügig ausgelenkt und der Dämpfer folgt schnell. Hier dominieren daher die viskosen Widerstände. Die vorhandenen elastischen Anteile (kleine Auslenkung der Feder) zeigen sich dann als Normalspannungen (siehe Kap. 5).

Die obige Kombination aus viskosem und elastischem Verhalten bezeichnet man als viskoelastisches Verhalten. Während der viskose Teil gut mit den Messungen aus Kap.2 beschrieben werden kann, sind für die Charakterisierung der elastischen Eigenschaften weitere Untersuchungen erforderlich. Auf diese wird in den folgenden Abschnitten eingegangen.

3.2. Relaxationversuch

Zunächst sei der sogenannte Relaxationsversuch betrachtet. Dabei wird ein Material plötzlich mit einer Scherung g verschert. Das Material reagiert auf die Scherung mit einer Schubspannung t(t). Der Versuch kann beispielsweise mit einem Kegel-Platte-System realisiert werden. Dazu wird der Kegel um einen bestimmten Betrag verdreht und das Drehmoment als Maß für die Schubspannung als Funktion der Zeit gemessen.

Ein rein viskoses Fluid zeigt nur bei einer sich ändernden Scherung (Schergradient 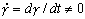) eine Schubspannung. Dies gilt beim Relaxationsversuch nur beim Anfangssprung von 0 auf g. Danach ist das System sofort im Gleichgewicht und die Schubspannung geht wieder auf 0 zurück. Das System hat sich in unendlich kurzer Zeit entspannt (relaxiert). Dieses Verhalten ist in der Abb.3.2.1 als gestrichelte Linie angedeutet.


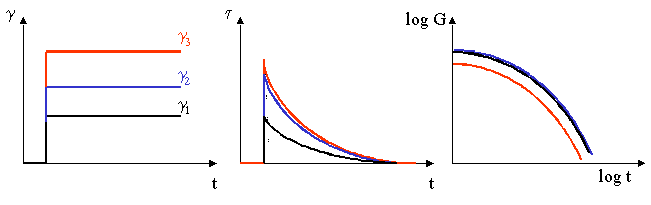
Abb. 3.2.1 - Zeitliche Verläufe von Scherung, Schubspannung und Schubmodul beim Relaxationsversuch

Bei einem viskoelastischen Fluid ergibt sich ein abweichendes Bild, welches bei Betrachtung des Feder-Dämpfer-Modells deutlich wird. Die sprunghaft einsetzende Deformation wird zunächst von der Feder aufgenommen und streckt diese. Erst danach beginnt die Bewegung des Dämpfers und entspannt dabei die Feder, bis das Material vollkommen entspannt ist. Am Beginn der Deformation (Scherung) wird der Widerstand des Materials also durch die elastischen Kräfte bestimmt. Diese können durch das HOOKEsche Gesetz beschrieben werden :

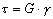
G ist dabei das sogenannte Schubmodul und in diesem Fall auch Relaxationsmodul. Dieses kann aus den gemessenen t und g ermittelt werden und ist ebenfalls in der Abbildung 3.2.1 als zeitlicher Verlauf jedoch logarithmisch dargestellt :

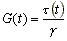
Zu Beginn der Messung erhält man ein maximales Relaxationsmodul G(t=0)=G0 , welches vorwiegend die elastischen Eigenschaften beschreibt. Mit einsetzender viskoser Deformation entspannt sich die Feder und der elastische Widerstand sinkt. Entsprechend sinkt auch das Relaxationsmodul über der Zeit. Der zeitliche Verlauf des Moduls kann in einfachster Form mit einer Exponentialfuntion der Form :


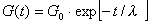
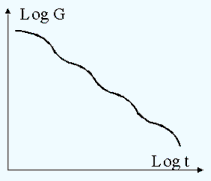
Abb.3.2.2.- Schubmodulverlauf bei komplexen Polymeren mit Relaxationszeitspektrum

beschrieben werden. Die Größe l wird als Relaxationszeit bezeichnet. Polymere Materialien können meist nicht als einfache Reihenschaltungen einer Feder und eines Dämpfers betrachtet werden. Vielmehr sind es Verschaltungen mehrerer Feder-Dämpfer-Systeme. Der Verlauf des Schubmoduls wird entsprechend kompliziert (Abb.3.2.2). Jedoch lässt sich ein derartiger Verlauf beschreiben durch :

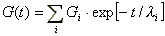
Das Material besitzt dann nicht nur eine charakteristische Relaxationszeit, sondern eine Relaxationszeitsprektrum.

Bei sehr kleinen Scherungen ist das Schubmodul G unabhängig von der Größe der Scherung, d.h. die Funktionen G(t) sind gleich (schwarze und blaue Linien in Abb.3.2.1) In diesem Fall gilt der lineare Zusammenhang zwischen Schubspannung und Scherung nach dem HOOKEschen Gesetz. Man spricht hier auch von einer linearen Viskoelastizität des Materials. Diese findet man bis zu einer maximalen bzw. kritischen Scherung gc. Die Feder kann nur bis zu diesem Betrag eine Scherung durch elastische Deformation aufnehmen. Verdreht man das Material über diesen Grenzwert hinaus, dann steigt die Schubspannung nicht mehr nach dem Hookeschen Gesetzt linear mit der Scherung an. Bei der Bildung dieses Schubmoduls G(t) liegen die Kurven dann unterhalb der Kurven für g<gc (rote Kurve in Abb.3.2.1.). Dieses Verhalten, bei dem Schubspannung und Scherung nichtlinear miteinander verbunden sind, wird als nichtlineare Viskoelastizität bezeichnet.

3.3. Kriechversuch
Beim Relaxationsversuch wird die Probe plötzlich verschert und die Entwicklung der Schubspannung über der Zeit beobachtet. Im Gegensatz dazu wird beim Kriechversuch plötzlich eine Schubspannung auf die Probe angewandt und die resultierende Deformation der Probe erfasst (Abb.3.3.1). Die Betrachtung des Feder-Dämpfer-Modells sagt voraus, dass die plötzlich einsetzende Kraftwirkung zunächst die Feder spannt. Der Dämpfer bewegt sich erst nach und nach. Dies bedeutet, dass zunächst eine elastische Deformation ohne zeitliche Verzögerung einsetzt. Die viskose Deformation setzt ein, wenn die elastische Deformation ausgereizt ist. Dann erfolgt eine kontinuerliche Verscherung der Probe mit konstanter Schergeschwindigkeit. Der resultierende Verlauf der Scherung g als Funktion der Zeit ist in Abb. 3.3.1 dargestellt.


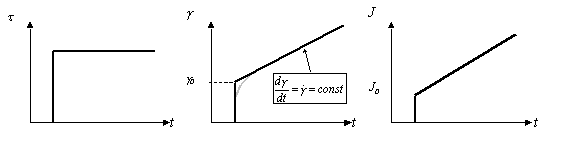
Abb.3.3.1- Zeitlicher Verlauf von Schubspannung, Scherung und Kriechnachgiebigkeit beim Kriechversuch

In Anlehnung an die Auswertung des Relaxationsversuchs wird beim Kriechversuch eine Quotient aus gemessener Scherung und angelegter Schubspannung, die sogenannte Kriechnachgiebigkeit J, gebildet :

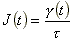
Auch der Verlauf dieser Größe ist in der Abb. 3.3.1 dargestellt. Der Verlauf kann näherungsweise durch eine lineare Funktion der Form J(t)=J0+A t beschrieben werden. Der erste Term J0, die stationäre Kriechnachgiebigkeit, umschreibt die rein elastische Deformation. Bei einem Relaxationsverhalten mit einfacher Relaxationszeit l entspricht die Größe J0 dem inversen Schubmodul G0 aus dem Relaxationsversuch. Der zweite Term umschreibt die viskose Deformation. Die Änderung der Scherung bei viskoser Deformation wird durch die Viskosität beschrieben : Dg/Dt=t/h0. Die Viskosität h0 ist die sogenannte Nullscherviskosität, d.h. die Viskosität bei verschwindender Deformationsgeschwindigkeit. Insgesamt ergibt sich damit folgende Funktion zur Beschreibung des Kriechversuchs :

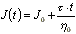
Die elastische Deformation beim Kriechversuch ist reversibel. Entsprechend wird nach dem Weglassen der Schubspannung eine Rückstellung des Materials (Zurückdrehen) erfolgen. In der Messung der Scherung äußert sich dies in einem Absinken der Scherung nach der Entspannung (Abb.3.3.2). Der Betrag der Scherungsänderung, bezogen auf die applizierte Schubspannung, ergibt die sogenannte Kriecherholung, auch Retardation genannt :

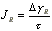
Es ist ein weiteres Maß für die Beschreibung der elastischen Deformationen im Material und sollte bei vollkommen ausgebildeter Scherdeformation genau der stationären Kriechnachgiebigkeit J0 entsprechen.

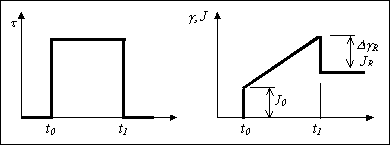
Abb.3.3.2 - Funktionsverläufe bei der Kriecherholung

3.4. Oszillationsmessung
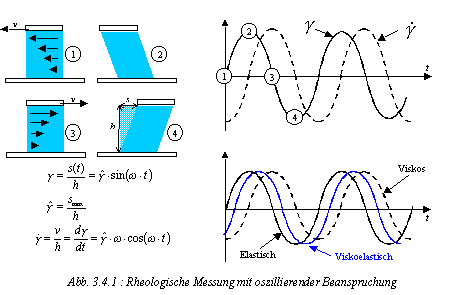
Eine elegante Art, viskose und elastische Eigenschaften eines Materials zu ermitteln, sind Messungen unter oszillierender Beanspruchung (Schwingungsmessung). Dazu wird das Material meist einer sinusförmigen Deformation mit kleiner Amplitude ausgesetzt. Die kleine Amplitude garantiert dabei die Messung im linearen viskoelastischen Bereich. In Abb. 3.4.1 ist das Messprinzip dargelegt. Die Probe wird ausgehend vom Ausgangszustand 1 bis zu einer maximale Auslenkung smax entsprechend einer maximalen Deformation verschert (Punkt 2). Danach setzt die Gegenbewegung ein, wobei die höchste Geschwindigkeit am Punkt 3 erhalten wird. Am Punkt 4 erfolgt dann die erneute Umkehrung der Bewegung. Die Deformation wird durch eine Sinusfunktion beschrieben, die durch die zwei Parameter Amplitude und Kreisfrequenz w charakterisiert ist. Die Kreisfrequenz ergibt sich dabei aus der Frequenz der Schwingung f nach w=2*p*f.



Der zeitliche Verlauf der Scherdeformation kann durch die dargestellte Sinus-Funktion beschrieben werden. Die Schergeschwindigkeit ergibt sich dann als Ableitung dieser Sinus-Funktion und zeigt einen um 90° phasenverschobenen Verlauf.
Ein ideal elastisches Material hat einen Widerstand proportional zur Scherung (HOOKEsches Gesetz) mit dem Proportionalitätsfaktor Elastizitätsmodul G´. Seine Antwort auf eine sinusförmige Deformation ist entsprechend :

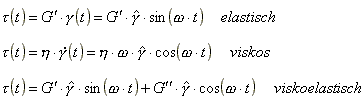
Hingegen hat ein ideal viskoses Material einen Widerstand proportional der Schergeschwindigkeit mit dem Proportionalitätsfaktor Viskosität. Der Term h*w wird auch als Verlustmodul G´´ bezeichnet. Ein viskoelastisches Material mit sowohl elastischem als auch viskosem Verhalten zeigt entsprechend eine Kombination beider Anteile.
Ein elastisches Fluid hat einen Widerstand, der in Phase mit der Scherdeformation liegt, während bei einem viskosem Fluid der Widerstand um 90° phasenverschoben zur Scherdeformation verläuft. Ein viskoelastisches Fluid hat daher eine Phasenverschiebung d, die zwischen 0 und 90° liegt und sich zu tan d=G``/G` ergibt. Sie ist ein Maß für die Anteile beider Verhaltensweisen am Widerstand. Die Gleichung für den Schubspannungsverlauf kann mit der Phasenverschiebung auch wie folgt formuliert werden :

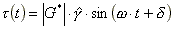
wobei |G*| der Betrag des sogenannten komplexen Moduls G* ist, welches sich aus dem realen, in Phase mit der Deformation befindlichen elastischen Anteil G`und dem 90° phasenverschobenen, imaginären Anteil G `` zusammensetzt :

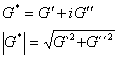
In Analogie zum komplexen Modul G* kann auch eine komplexe Viskosität h*=h´+ih`` gebildet werden mit h`=G``/w und h``=G`/w. Der Betrag der komplexen Viskosität |h*| für eine Deformationsfrequenz w entspricht dabei der stationären Scherviskosität bei einer Schergeschwindigkeit von 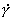=w (COX-MERZ-Beziehung).
Die Module G´ und G´´ sind keineswegs konstante Stoffgrößen. Sie verändern sich mit Amplitude und Frequenz der angelegten Deformationsfunktion. Entsprechend werden bei Messungen häufig Bereiche dieser beiden bestimmenden Parameter durchfahren, wobei man bei variabler Amplitude von einem Amplituden-Sweep und entsprechend bei variabler Frequenz von einem Frequenz-Sweep spricht. Ein typischer Verlauf der Module als Funktion von Frequenz und Amplitude ist in Abb.3.4.2 dargestellt.

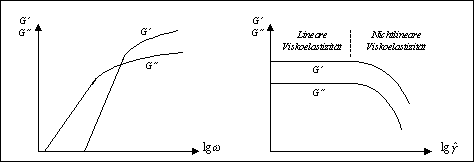
Abb. 3.4.2 - Typische Verläufe von Speicher- und Verlustmodul als Funktion von Frequenz und Amplitude

Zunächst sei die Darstellung des Amplituden-Sweeps betrachtet. Bei kleinen Amplituden bleiben die gemessenen Module konstant, man befindet sich im linear-viskoelastischen Bereich. Der Übergang in den nichtlinear-viskoelastischen Bereich zeigt sich in der Veränderung der Module. Ein Amplitudensweep lässt sich demnach gut zur Identifizierung des Übergangs nutzen.
Die häufigste Versuchsart bei Schwingungsmessungen ist jedoch der Frequenzsweep. Er liefert häufig Verläufe entsprechend Abb.3.4.2 links.
Bei kleinen Frequenzen dominiert der viskose Widerstand entsprechend einem hohen Verlustmodul. Der Anstieg des Verlustmoduls dG``/dw für w®0 definiert die sogenannte Nullviskosität h0. Der Speichermodul steigt mit steigender Frequenz schneller an und übersteigt ab einer gewissen Frequenz den Verlustmodul. Ab hier dominieren die elastischen Anteile am Widerstand. Ähnlich wie beim Relaxationsversuch lässt sich das frequenzabhängige Verhalten der Module durch ein Relaxationszeitspektrum beschreiben. Danach ergeben sich die Module nach :

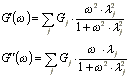
Eine gemessene Frequenzabhängigkeit der Module wird häufig durch ein Relaxationszeitspektrum mit äquidistanten Relaxationszeiten beschrieben (siehe auch M.Pahl et.al. "Praktische Rheologie der Kunststoffe und Elastomere",VDI-Verlag, Düsseldorf, 1995).

Die charakteristischen Größen der Schwingungsrheometrie werden durch verschiedene Stoffeigenschaften bestimmt.
Insbesondere Molmasse und Struktur der Moleküle sowie deren Vernetzung spielen eine große Rolle. Nur wenige quantitative Zusammenhänge existieren zwischen Materialgrößen und rheologischen Größen. Eine der wenigen Ausnahmen stellt die Nullviskosität h0 dar, deren Abhängigkeit von der Molmasse MW des Polymers gut definiert ist. Es gilt :

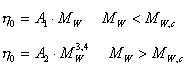
Sind für ein Material die beschreibenden Größen A1, A2 bzw.MW,c bekannt, dann kann aus der Messung der Nullviskosität schnell und einfach auf die Molmasse des Materials geschlossen werden. Dies ermöglicht einfache Regelungen in der Polymerverarbeitung.

Schwingungsmessungen können prinzipiell mit allen gängigen Rheometer-Systemen durchgeführt werden, vorausgesetzt die Mechanik und Elektronik lassen dies zu. Bei der Messung werden die Anteile des Drehmoments in Phase sowie des 90° phasenverschobenen Anteils ermittelt und ausgewertet (siehe hierzu auch W.-M. Kulicke "Fließverhalten von Stoffen und Stoffgemischen",Hüthig und Wepf Verlag, Basel, 1986, S.91 ff.).